Penyelesaian sistem persamaan x 3y – z = 12 2x – y z = 0 3x y – 2z = 11 Post a Comment Penyelesaian sistem persamaan x 3y – z = 12 2x – y z = 0 3x y – 2z = 11 adalah x, y, dan z Nilai dari xy yz – xz = A 3 Corresponding elements are equal 3x = x 4 3y = 6 x y 3z = 1 – z w 3w = 2w 3 (1) (2) Solving equation (1) 3x = x 4 3x – x = 4 2x = 4 x = 4/2 x = 2 Solving equation (2) 3y = 6 x y 3y – y = 6 x 2y = 6 x Putting x = 2 2y = 6 2 2y = 8 y = 8/2 y = 4 Solving equation (4) 3w = 2w 3 3w – 2w = 3 w = 3 Solving equation (3) 3z = – 1 z w 3z – z = – 1 w 2z = – 1 w Putting w = 3 2z = – 1 3 2z = 2 z = 2/2 z = 1 Hence, x = 2, y = 4 , w = 3 & zYou can put this solution on YOUR website!
Lim X Y Z Rightarrow 0 0 0 Xyz X 3 Y 3 Chegg Com
(x y z)^3-x^3-y^3-z^3
(x y z)^3-x^3-y^3-z^3-Y=xz/3 Simple and best practice solution for y=xz/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itYep, that can't be when you change 2(xyz)=3(xyz) to 2=3, you divide both paths of the equation by xyz, which, as you know is zero Division by zero is an illegal operation You can get all sorts of false results by dividing by zero



If X Y Z 9 Then Find The Value Of 3 X 3 3 Y 3 3 Z 3 3 3 X 3 Y 3 Z Mathematics Topperlearning Com
Solution Verified by Toppr x 3y 3z 3−3xyz=(xyz)(x 2y 2z 2−xy−yz−zx) First take LHS (xyz)(x 2y 2z 2−xy−yz−zx) To multiply two polynomials, we multiply each monomial of one polynomial (with its sign) by each monomial (with its sign) of the other polynomial We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0,x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx)x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro (टीचू) MathsNo integers x;y;z with xyz6= 0 satisfy x3 y3 z3 = 0 Proof We may assume that x, y, and zare pairwise coprime If xyzis not divisible by 3, then the equation has no solution even in Z=(9), where every nonzero cube is 1 Suppose then, without loss of generality, that 3jz We will work in the UFD R= Z with = ( 1i p 3)=2, a root of the
If x, y, z are different and Δ = (x, x2, 1 x3), (y, y2, 1 y3), (z, z2, 1 z3) = 0 then show that 1 xyz = 0 We have Now, we know that If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants So we can try our methods to factor a polynomial of degree 3 over an integral domain If it can be factored then there is a factor of degree $1$, we call it $zu(x,y)$ and $u(x,y)$ divides the constant term of $p(z)$ which is $x^3y^3$Verify the Property X × (Y Z) = X × Y X × Z by Taking X = − 3 7 , Y = 12 13 , Z = − 5 6 Mathematics Advertisement Remove all ads Advertisement Remove all ads
9x 15y 108 = −48x −8y 76 57x 23y = 184 Now we do a similar procedure using this and the third equation (the one that never had the z in it) 57x 23y = 184 AND 9x3y=25 Pick a variable to solve both equations for and then set them equal, which will give you just one variableStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x2yz=6;2xy3z=3;x3y3z=10 Tiger Algebra Solver Get an answer for 'Solve the following system of equations 3x 2y z = 1, x y z = 4 and 2x 2y 3z = 8' and find homework help for other Math questions at eNotes




If X Y Z 0 Show That X3 Y3 Z3 3xyz Scholr



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora
(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xyAlgebracalculator x2yz=0, 2xyz=1, 3xy2z=5 en Related Symbolab blog posts Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic solvingX^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2}




X 3 Y 3 Z 3 3xyz の因数分解についての話題から 身勝手な主張




Phan Tich đa Thức Thanh Nhan Tử X Y Z 3 X3 Y3 Z3 Hoc24
Systemofequationscalculator xyz=25, 5x3y2z=0, yz=6 es Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations In this post, we will learn how Swagat Swargari, added an answer, on 19/5/15 Swagat Swargari answered this Using identity a 3 b 3 c 3 3abc = (abc) (a 2 b 2 c 2 ab bc ca) (xy) 3 (yz) 3 (zx) 3 3 (xy) (yz) (zx) = (xy yz zx) (xy) 2 (yz) 2 (zx) 2 (xy) (yz) (yz) (zx) (zx) (xy) = (2x 2y 2z) x 2 y 2 2xy y 2 z 2 3 x y z, x² y³ z`, 10 x y² z³ Recibe ahora mismo las respuestas que necesitas!



X3 Y3 Identity




Phan Tich đa Thức Thanh Nhan Tử A X Y Z 3 X 3 Y 3 Z 3 B 8 A B C 3 X Y 3 Y
Piece of cake Unlock StepbyStep Natural Language $2(x^3y^3z^3)6xyz=5$ denkleminde $x^3y^3z^3=3$ eşitliğini yerine yazarsak $xyz=\frac{1}{6}$ eşitliği bulunur Bu sefer 3 farklı denklemimiz var $(xyz)^4=x^4y^4z^44(x^3zx^3yxy^3y^3zxy^3xz^3)$So in this problem we are given f of X Y Z is equal to x Y square, it said, okay, so now we need to find our gradient So our gradient is a vector that's made up of all the partial derivatives So DF dx d f d Y and D f D said, okay, so let's find your partial derivatives z)=x^{3} y^ 0124 In Exercises $18,$ describe how the graph of




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



If X Y Z 9 Then Find The Value Of 3 X 3 3 Y 3 3 Z 3 3 3 X 3 Y 3 Z Mathematics Topperlearning Com
Answer is (x 1)/3 (y 2)/1 = (z 4)/1 Given that the line passes through (1, 2, 4) and this point also lies on the given plane Thus, required line will be in the form of (x 1)/l = (y 2)/m = (z 4)/n Any point on the given line is (r 1 1, 3r 1 2, rPlot x^2 y^3, x=11, y=03 WolframAlpha Volume of a cylinder?Move all terms containing x to the left, all other terms to the right Add 'y' to each side of the equation 3x 1y y = y z Combine like terms 1y y = 0 3x 0 = y z 3x = y z Divide each side by '3' x = y z Simplifying x = y z




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube
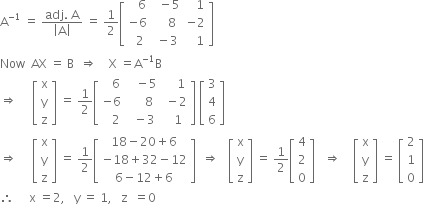



Use Matrix Method To Solve The Following System Of Equations X Y Z 3x 2y 3z 4x 4y 9z 6 Zigya
Let's have a example x ≥ 0, y ≥ 0, z ≥ 0, x y z = 1, find max of x 2 y y 2 z z 2 x you may think x = y = z = 3 1 is the point of max, but the real one is x = 3 2 , y = 3 1 , z = 0 or The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X3 Y3 Z3 − 3XYZ − W3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S(Q) is dense in S(R) Observe that S has a singular rational point PFactor (yz)^38 (y z)3 − 8 ( y z) 3 8 Rewrite 8 8 as 23 2 3 (yz)3 −23 ( y z) 3 2 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = yz a = y z and b = 2 b = 2 (yz− 2)((yz)2 (yz)⋅2 22) ( y z 2




The Monoids Z X 3 Y 3 5 Xyz Z 3 X Y And Z X 3 Y 3 5 Download Scientific Diagram



Www Jstor Org Stable
Find the point on the plane x − y z = 8 that is closest to the point (1, 3, 6) This what I have so far Z = 8xy d = Sqrt ((x1)2 (y3)2 (z6)2) f(x,y,z) = d2 = (x1)2 (y3)2 (z6)2 Substitute for z = (x1)2 (y3)2 (2xy)2 Not sure how to move forwardThe maximum possible value of x^3y^3y^3z^3z^3x^3 has the form \dfrac {a} {b}, where a and b are positive, coprime Let x,y,z be nonnegative real numbers satisfying the condition x y z = 1 The maximum possible value of x3y3 y3z3 z3x3 has the form ba , where a and b are positive, coprime https//wwwquora x=21/2 y=4 z=11/2 xyz=1 x2y3z=2 xz=5 Primero hay que resolver la ecuacion para x xz=3 x=5z Ahora hay que sustituir los valores de x
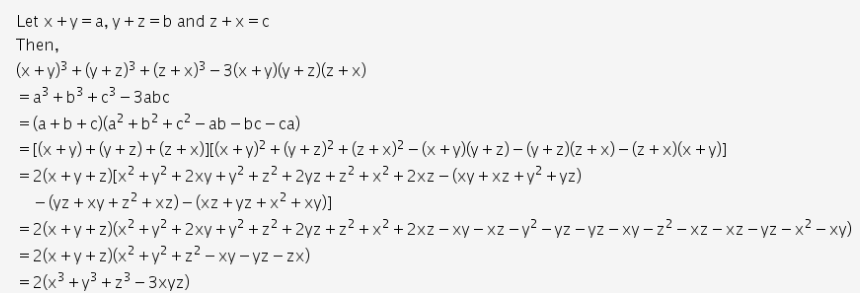



X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Cbse Class 9 Maths Learn Cbse Forum
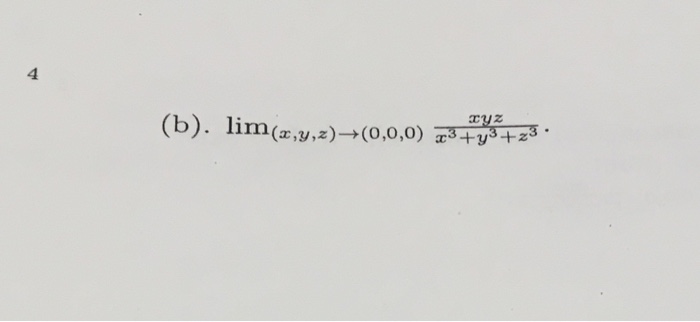



Lim X Y Z Rightarrow 0 0 0 Xyz X 3 Y 3 Chegg Com
(xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agreePiece of cake Unlock StepbyStep Natural LanguageNonzero x 3y 2 via lattice reduction, ANTS IV (00) * 39 D R Heathbrown, W M Lioen, and H J J Te Riele,On Solving the Diophantine Equation x 3 y 3 z 3 =k on a Vector Computer, Math Comp 61(1993), * 52 Eric Pine, Kim Yarbrough, Wayne Tarrant and Michael Beck, University of Georgia * 75 Andrew Bremner (1993)




3x 3y Rule Beckyparker




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube
Evaluate the following java expression,if x=3,y=5 and z=10 zyyzx Vidya t v Evaluate the following java expression,if x=3,y=5 and z=10 zyyzx Posted on by Views Score Share EngineeringCS EngineeringIS mca JIT Davangere SEMVI Java × Predict today's top selflearner and win assured reward It's FREE JUST A CLICK if x1/x=5,then find value of x^31/x^3 The valuesof 249square 248square is 729X3512y3 Factorise (abc)³a³b³c3 I need very urgently please answer as quickly as you can Rich Text Editor, question_data2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3 2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin




X 3 Y Z Y 3 Z X Z 3 X Y Clearnote
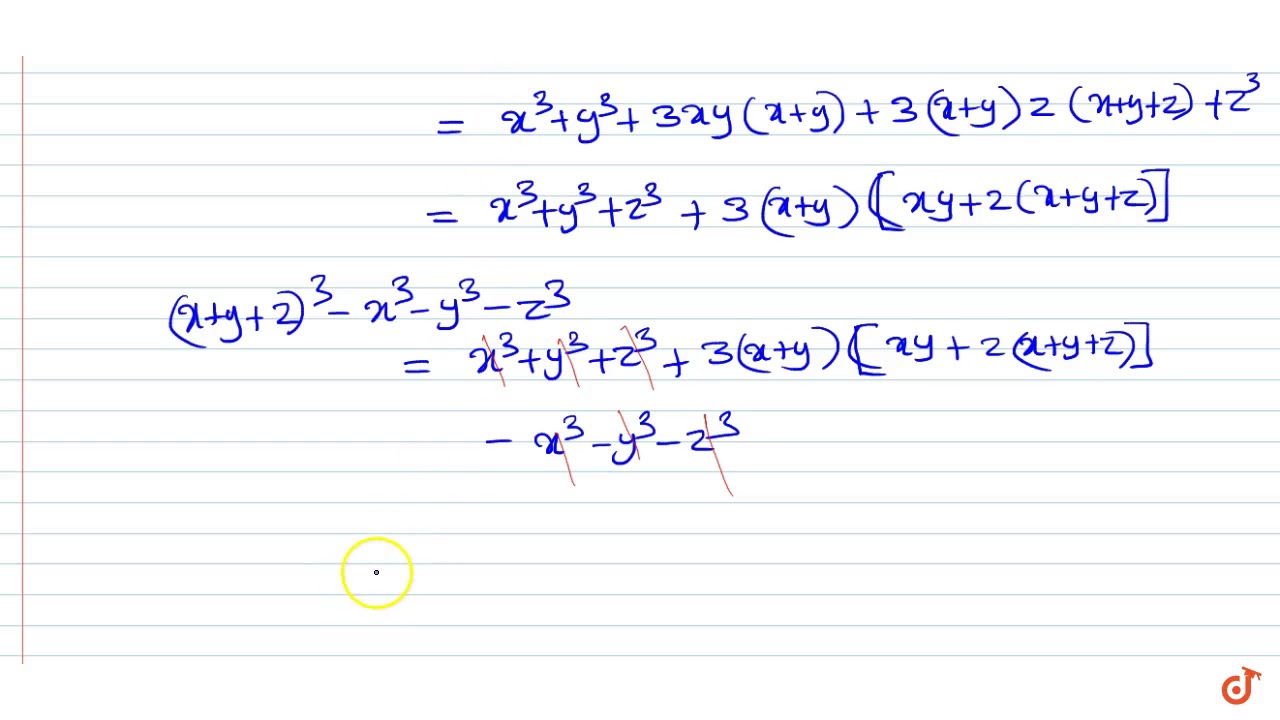



Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube
Object17 x = 1 , y = 2 , z = 3,则表达式 y+=z--/++x 的值 1 z是以原值运算的(也就是3) 2 而 x 的值是1 后再进行运算的(11) 3 还有一点就是整数除以整数的结果永远是整数 4 = 是把左边(y)和右边的值( z--/++x )相加并赋值给左边的 y,既 y = 341 Factoring x 3 yx 3 zxy 3 xz 3 y 3 zyz 3 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 y 3 zxy 3 Group 2 x 3 yx 3 z Group 3 xz 3yz 3 Pull out from each group separately Group 1 (xz) • (y 3) Group 2 (yz) • (x 3) Group 3 (xy) • (z 3) Looking for common subexpressionsयदि (x y) 1/3 (y z) 1/3 = (z x) 1/3 है, तब (x 3 y 3 z 3) Twelve sticks, each of length one unit, are used to form an equilatera बारह डंडियों में से, प्रत्येक की लम्बाई एक इकाई है, जिनका उपयोग समबाहु



If X Y Z 0 Show That X3 Y3 Z3 3xyz




Question 3 25 Marks A Find Az And Z For X3 Y3 Chegg Com
Solve x y z = x 3 y 3 z 3 = 8 in Z First I tried to transform this equation, substituting x = 8 − y − z So I end up with x 3 y 3 z 3 = 8 ( 8 − y − z) 3 y 3 z 3 = 8 Using Wolfram Alpha I expanded this equation and tried to factorize it so finally I got ( z − 8) ( y 2 y ( z − 8) − 8 z) = 168Cho x, y, z là 3 số dương thỏa mãn xyz=3 CM \frac{x}{x\sqrt{3xyz}}\frac{y}{y\sqrt{3yxz}}\frac{z}{z\sqrt{3zyx}}\leq 1There are infinite solutions as you have 3 variables but only one equation However, it is interesting to note that there is no solution for which all of the varibles x,y,z are integersFermat's last theorem says that there is no solution of x^n
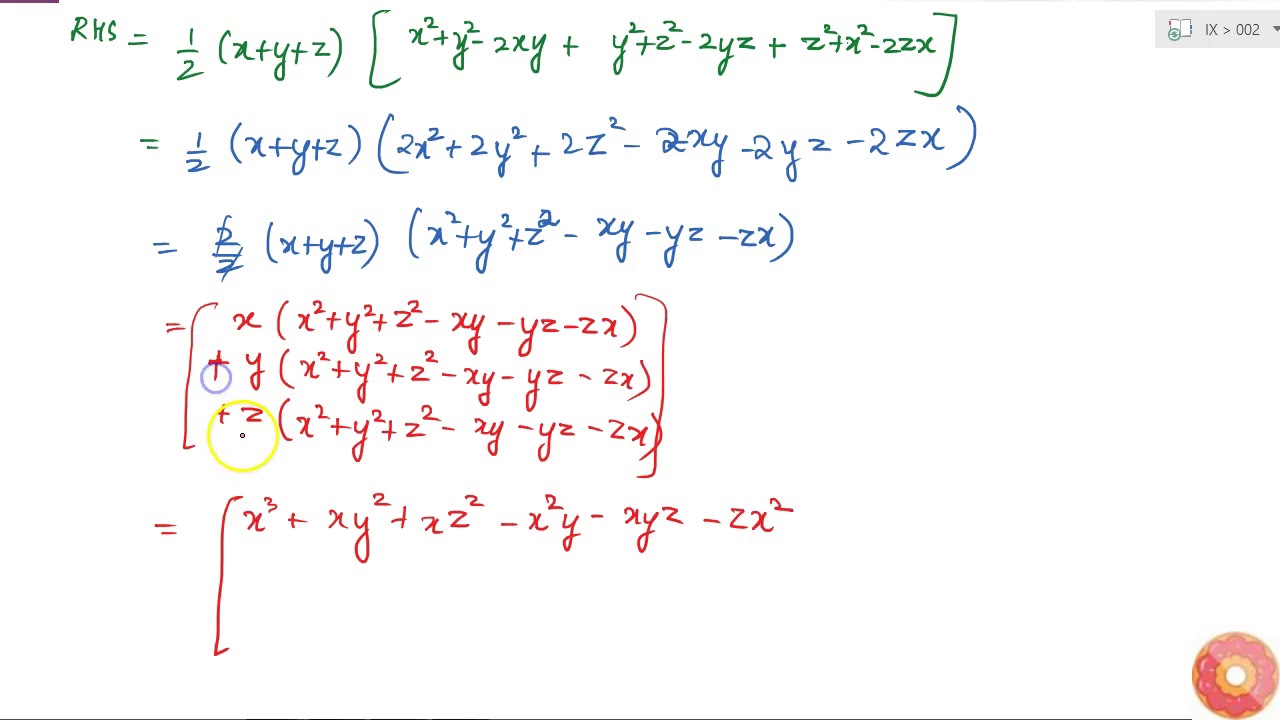



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




3x 3y Rule Beckyparker
X^3 x^2 y x y^2 y^3 WolframAlpha Volume of a cylinder? View Full Answer Deep Sah, added an answer, on 3/10/15 Deep Sah answered this We know that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ac) Take, a = xy, b = yz, c = zx we get, (xy)^3 (yz)^3 (zx)^3 3 (xy) (yz) (zx) Use sum of cubes identity to find x^3y^3z^3 = (xyz)(x^2y^2xyzz^2) Use the sum of cubes identity a^3b^3=(ab)(a^2abb^2) with a=xy and b=z as follows x^3y^3z^3 =(xy)^3z^3 =((xy)z)((xy)^2(xy)zz^2) =(xyz)(x^2y^2xyzz^2)




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5



X3 Y3 Formula
On x^3 x y^3 y = z^3 z On x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1)where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uvSolve by Substitution 2xyz=3 , 3xy3z=3 , x3y2z=3, , Move all terms not containing to the right side of the equation Tap for more steps Subtract from both sides of the equation Add to both sides of the equation Replace all occurrences of with in each equation Tap for more stepsIt is usually phrased as w 3 x 3 y 3 =z 3 or w 3 x 3 =y 3 z 3, with the implication that the variables are to be positive, as in the integer solutions 3 3 4 3 5 3 =6 3 (an amusing counterpart of the classic identity 3 2 4 2 =5 2 but no, it does not generalize further) and 12 3 1 3 =10 3 9 3 =1729 (which famously occurs in the Ramanujan taxicab story)




Phan Tich đa Thức Thanh Nhan Tử X Y Z 3 X 3 Y 3 Z 3 Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải



If X Y Z 10 Xy Yz Zx 15 And Xyz 12 Then Find The Values Of I X 3 Y 3 Z 3 And Ii X 2 Y 2 Z 2 Sarthaks Econnect Largest Online Education Community
Find the x, y, and z intercepts {by substituting 0 in for the other variables} connect the three intercepts with a triangle Graph the equation x y z = 3 When a line intercepts an axis, the value of the other variables are zero xintercept x y z = 3 {the equation} x 0 0 = 3 {substituted 0 for y and z} x = 3 {combined like terms}X^3y^3z^33xyz=(xyz)(x^2y^2z^2xyyzzx)a^3b^3c^33abc=(abc)(a^2b^2c^2abbcca)a^3b^3c^33abc formula proofx^3y^3z^33xyz formula proofa




Ppt Polynomials Powerpoint Presentation Free Download Id
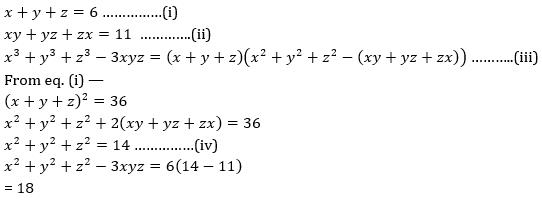



If X Y Z 6 And Xy Yz Zx 11 Then The Value Of X3 Y3 Z3 3xyz Isa 18b 36c 54d 66correct Answer Is Option A




If X Y Z Xyz Then 3x X 31 3x 2 3y Y 31 3y 2 3z Z 31 3z 2




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And X 3 Y 3 Z 3 7 Then The Value Of X 4 Y 4 Z 4 Is



Solved Solve The System X Y Z 3 2x Y 3 Select One Y 2x 3 6 3x B X 2x 3 6 3x C Z 2x 3 6 3x D No Solution E Course Hero




印刷可能 X 3 Y 3 X 3 Y 3 Identity




Factorise 27x 3 Y 3 Z 3 9xyz




Prove X Y Z 3 X 2 Y 2 Z 2 9 Therefore Y X Leqq 2 Sqrt 3 Mathematics Stack Exchange
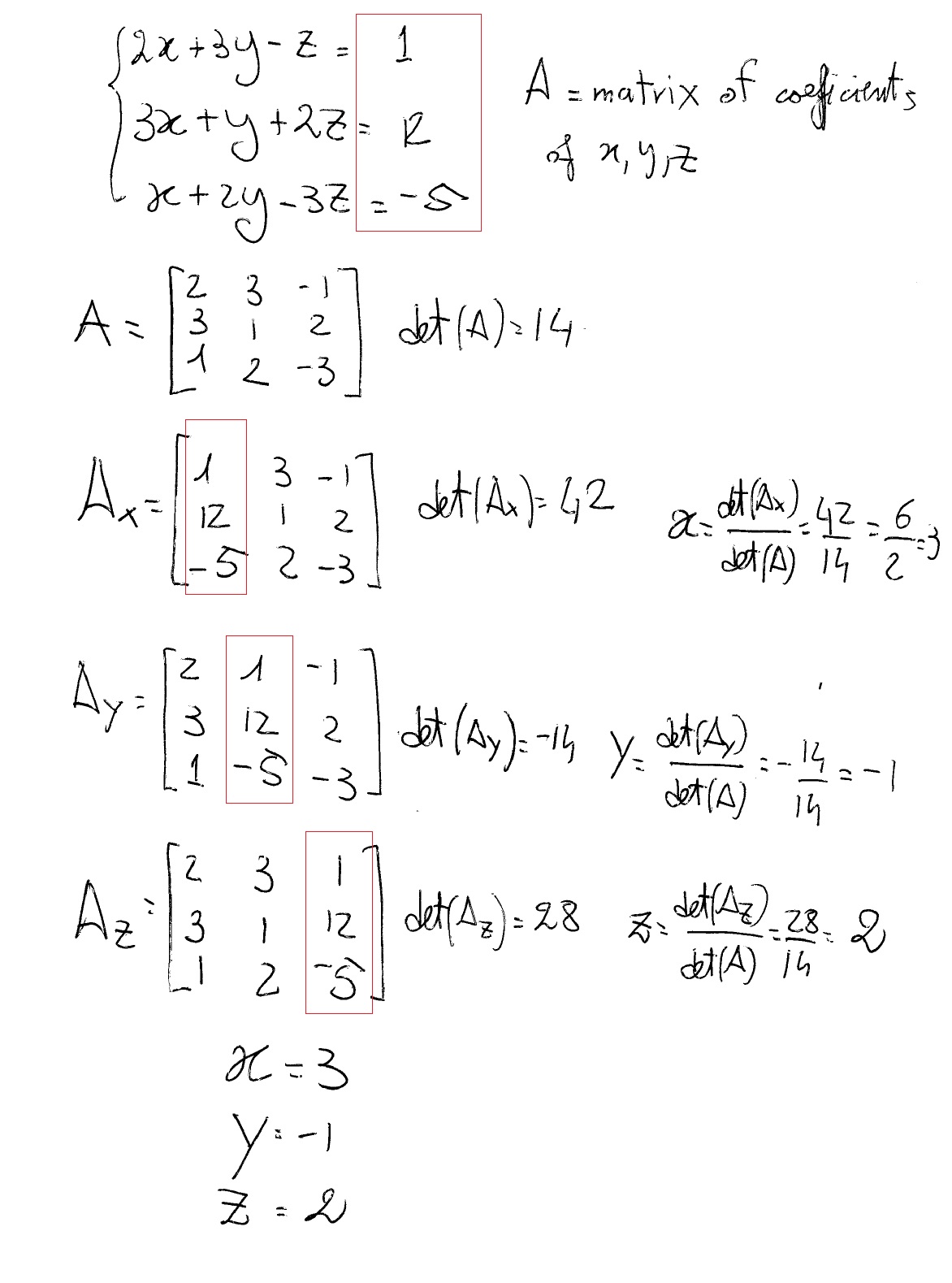



How Do You Solve 2x 3y Z 1 3x Y 2z 12 And X 2y 3z 5 Socratic




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z




Systems Of Linear Equations Let S Say You Need To Solve The Following For X Y Z 2x Y 2z 10 3x 2y 2z 1 5x 4y 3z 4 Two Methods Gaussian Ppt Download




Giải Toan Tren Mạng Giup Toi Giải Toan Hỏi đap Thảo Luận Về Toan Học Học Trực Tuyến Olm




If X Y Z 0 Then X 3 Y 3 Z 3 3 X Y Z Is Equal To A 0 B 6 X Y Z C 12 X Y Z D X Y Z




Graphing Software Fails To Include Point 1 1 1 In The Graph Of X 3 Y 3 Z 3 3xyz 0 Why Mathematics Stack Exchange




If X Y Z 1 Xy Yz Zx 1 Den Find The Maths Polynomials Meritnation Com



What Is X 3 Y 3 Z 3



Answer In Geometry For Tarynn Wiese




X3 Y3 Z3 3xyz X Y Z X Y 2 Y Z 2 Z X 2 Prove This Brainly In
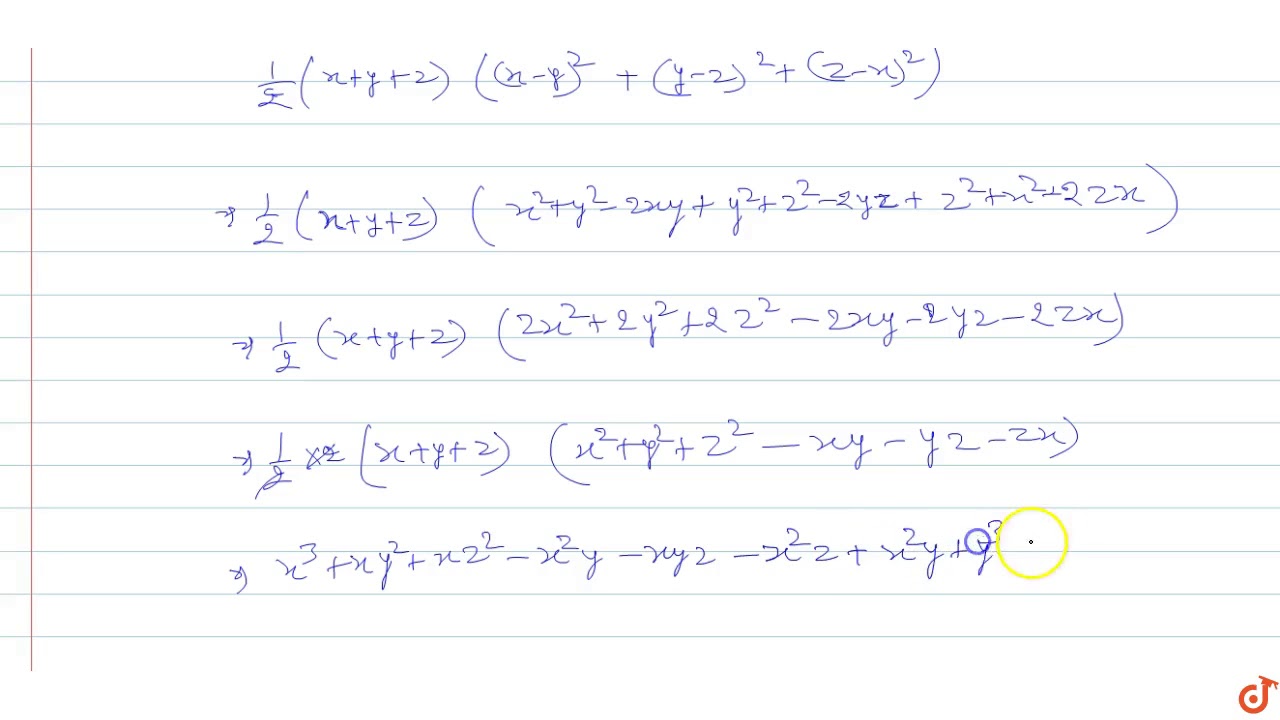



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Phan Tich đa Thức Thanh Nhan Tử X 3 Y 3 Z 3 3xyz Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải Bai Tập Toan Học




Solve The Following System Of Equations By Crout S Method X Y Z 3 2x Y 3z 16 And 3x Y Z 3 Mathematics 3 Question Answer Collection




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection



X三乗 Y三乗 Z三乗ー3xyzを丸暗記なしで因数分解するにはどうすればいいん Yahoo 知恵袋




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube




If X Y 2 2 X Y Z 4 And X2 Y Z2 3 So X3 Y Gauthmath




Giải Toan Tren Mạng Giup Toi Giải Toan Hỏi đap Thảo Luận Về Toan Học Học Trực Tuyến Olm
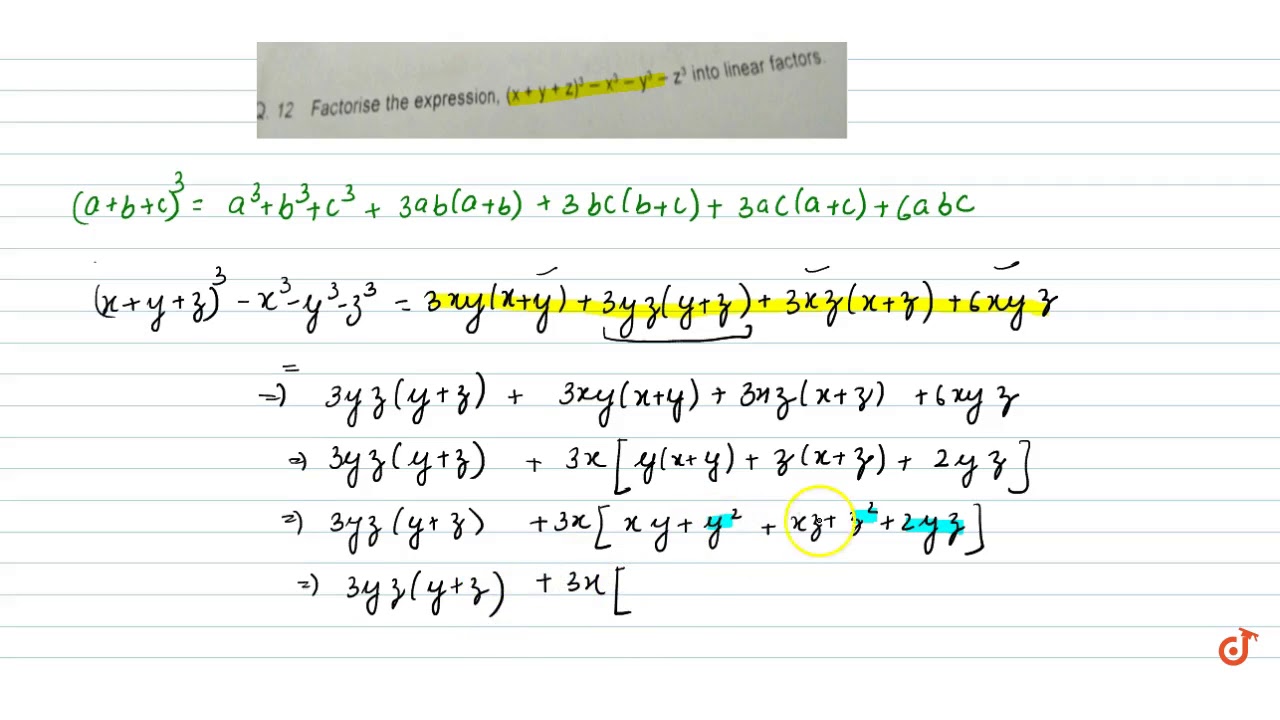



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube
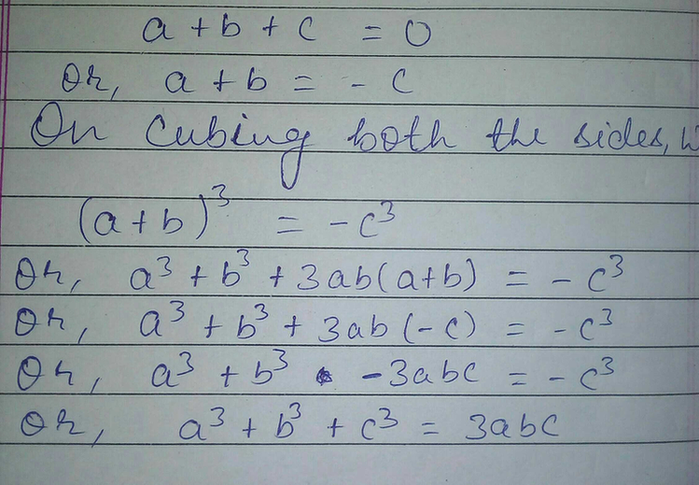



If X Y Z 0 Show That X3 Y3 Z3 3xyz Scholr




Chứng Minh X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Toan Học Lớp 9 Bai



3 Variable System Practice Flip Ebook Pages 1 2 Anyflip Anyflip




If Px Y Z X3 Y3 Z3 3 X Y Z And X B C A Y C A Gauthmath




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




Solve The Following System Of Equations By Crout S Method X Y Z 3 2x Y 3z 16 And 3x Y Z 3 Mathematics 3 Question Answer Collection




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




What Is X 3 Y 3 Z 3



1




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




If X Y Z 0 And X 3 Y 3 Xyz Y 3 Z 3 Xyz X 3 Z 3 Xyz A Then Which Of The Following Can Be A
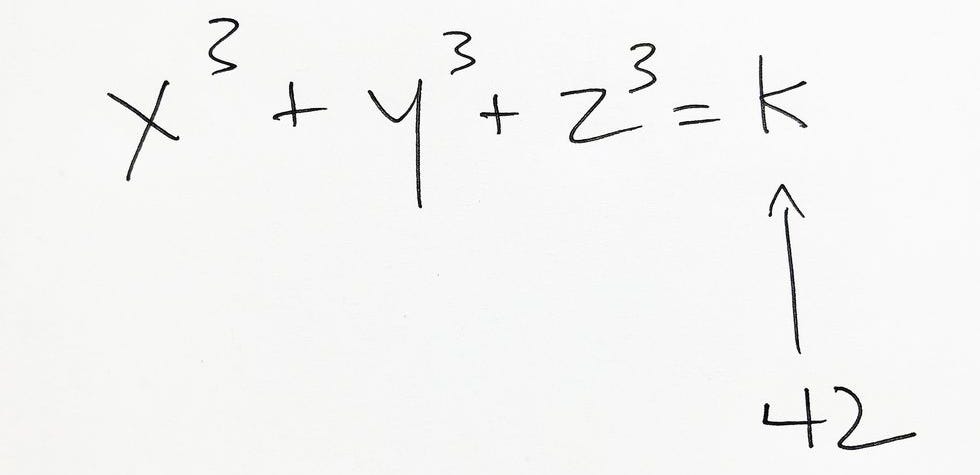



Hardest Math Problem Solved Diophantine Equation Answers




Q If X Y Z 1 Xy Yz Zx 1 And Xyz 1 Find The Value Of X3 Y3 Z3 Maths Polynomials Meritnation Com




With This Inequality Condition Xyz X Y Z 3 Mathematics Stack Exchange




How To Prove Xyz 1 3 Le X Y Z 3 Using Linear Algebra Mathematics Stack Exchange




3rdmath Flip Book Pages 251 287 Pubhtml5




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



Show That The Following System Of Equations Have X Y Z 3 X 2y 3z 4 X 4y 9z 6 By Rank Method Sarthaks Econnect Largest Online Education Community




If X Y Z 3 X2 Y2 Z2 5 X3 Y3 Z3 7 Then Find The Value Of X4 Y4 Z4 Maths Polynomials Meritnation Com




X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3 Youtube




If X Y Z 0 Then Find The Value Of X3 Y3 Z3 Brainly In




1 なんですけど なんでいきなりこの式が出てくるんですか 友達に聞いても Clearnote




18 Find The Value Of X3 Y3 Z3 Ifx Y Z 11 X2 Y2 Z2 45 And Xyz 40 Brainly In




If X Y Z And X X 3 X 4 1 Y Y 3 Y 4 1 Z Z 3 Z 4 1 0 Prove That Xyz Xy Yz Zx X Y Z




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com




Q32 Solve The System Of Equations X Y Z 3 X Y Z 3 Chegg Com




The Monoids Z X 3 Y 3 5 Xyz Z 3 X Y And Z X 3 Y 3 5 Download Scientific Diagram




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12
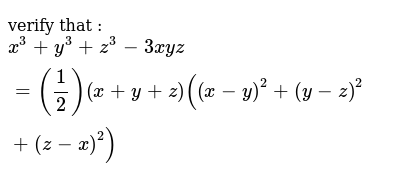



If X Y Z 0 Show That X3 Y3 Z3 3xyz




Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y Z 3 2 3y 5z 9



Www Nextgurukul In Questions Answers Forum Question Academic Prove X3 Y3 Z3 3xyz X Y Z X Y2



If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora
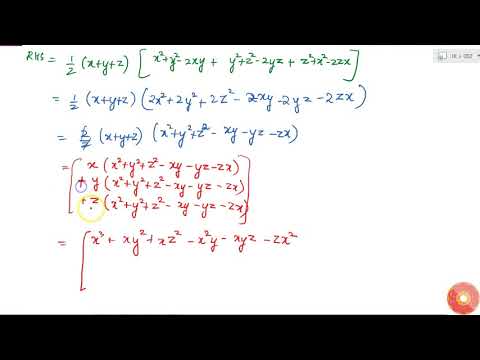



Verify That X 3 Y 3 Z 3 3x Y Z 1




Is 8 X 3 Y 3 Z 3 2 Ge 9 X 2 Yz Y 2 Xz Z 2 Xy True For Nonnegative Numbers Mathematics Stack Exchange




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Edurev Class 9 Question



Show That For All Real Numbers X Y Z Such That X Y Z 0 And Xy Yz Zx 3 Sarthaks Econnect Largest Online Education Community




If X Y Z 6 And Xy Yz Zx 12 Then Show That X3 Y3 Z3 3xyz Maths Polynomials 12 Meritnation Com



Solve The System Of Linear Equations By Matrix Method X Y Z 3 2x Y Z 2 X 2y 3z 2 Mathematics Topperlearning Com Dqx3252pp




X Y Z 3 2 X Y Z 6 X 2 Y 3 Z 2 Gauthmath




Solution Simplify X 2 Y 3 Z 2 3 X 3 Yz 3 1 2 Xyz 3 5 2




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download



How To Transform The Linear Equations X Y Z 6 2x Y 2z 10 3x 3y 4z 21 In A Matrix Equation And Solve Them By Finding The Inverse Of Coefficient Matrix Using The Adjoint Method Quora




If X Y Z 3 3 5 And X 3 Y 3 Z 3 1728 Then Find X Y Z




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z



Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community



Razlozhit Mnogochlen Na Mnozhiteli A X Y Z 3 X 3 Y 3 Z 3b X Y Z Xy Yz Zx Xyz Shkolnye Znaniya Com



How To Prove That Math X Y Z 3 27xyz Geq0 Math Quora
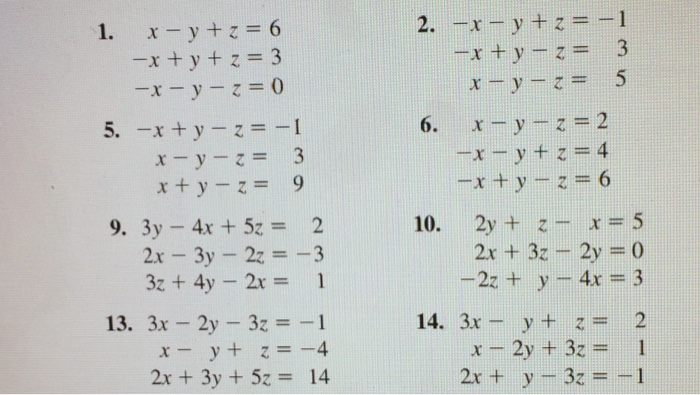



X Y Z 6 X Y Z 3 X Y Z 0 X Y Chegg Com



If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora



0 件のコメント:
コメントを投稿